√100以上 rsa 暗号 問題 138882-Rsa暗号 問題

暗号の10年問題 暗号技術は、その解析(解読)技術の進展およびコンピュータの計算能力の向上によって、時間と共 に安全性が低下する性質を持っている。 ⇒攻撃に要する計算量に基づいた「nビット安全性」として評価されている。Mar 06, 21 · RSA暗号の仕組みと安全性 レベル ★ マニアック 代数，情報・暗号理論 更新日時 公開鍵暗号方式の具体的なアルゴリズムであるRSA暗号の仕組みと安全性について解説します。 数学がまあまあ得意な高校生なら理解できるレベルの内容です。 目次 前提知識 RSA暗号の1字の簡単な暗号のRSA例題 公開鍵 n=9 (= 11 19) , e=7 秘密鍵 p=11, q=19 と d=13 平文 46 暗号文を平文から計算する 46 ^ 7 (mod 9) すなわち46を7乗し、それを9で割った余 りを求める。 暗号文 計算の結果は、84となる。

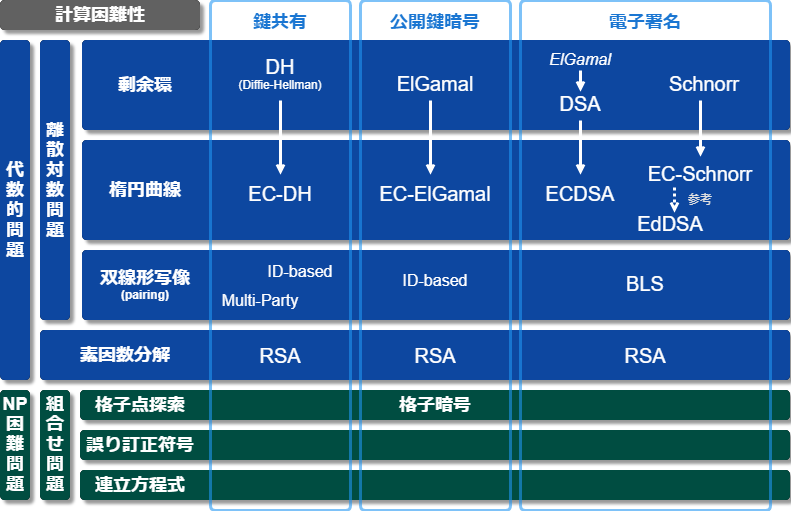
公開鍵暗号アルゴリズム Moxbox

Rsa暗号 問題

Rsa暗号 問題-RSA暗号とは RSAとは、後述する公開鍵暗号方式で使われる代表的な暗号アルゴリズムだ。1977年に発明され、以下の発明者の頭文字からRSAと名付けられた。 ロナルド・リベスト（Ronald Rivest） アディ・シャミア（Adi Shamir） レオナルド・エーデルマン（Leonard2 目次 1 暗号化方式 2 rsa 暗号化と復号化の方法 3 算術演算の時間評価 4 ヤヺキヨチデ互除法とエアョヺ関数

数学が役に立っている Rsa暗号の仕組みを解説 合同式とrsa暗号 第8回 Youtube

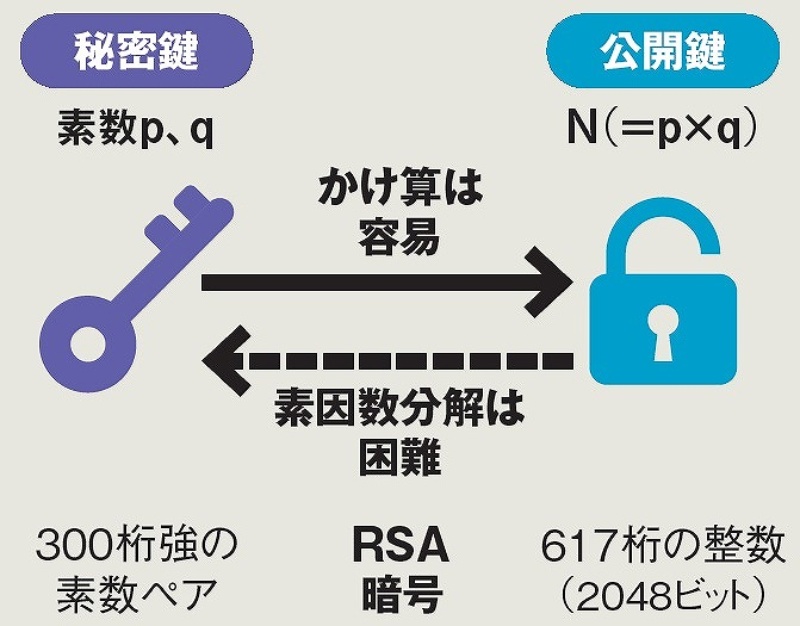
May 28,  · RSAとはインターネット通信で用いられる公開鍵暗号の1つです。 RSAは、2つの桁数が大きい素数をかけ合わせて積を求めるのは簡単でも、素因数分解が困難であるという非対称性により安全性を導き出したものです。Bkpctfのrsa暗号問題を解く CTF セキュリティ 16年3月4日に開催されたBoston Key Party CTFにチームm1z0r3として少しだけ参加した．大会からかなり日が経ってしまって今更感があるが，今回はbob's hatという RSA暗号 の問題のWriteupを書こうと思う．Rsa暗号（rsaあんごう）とは、桁数が大きい合成数の素因数分解問題が困難であることを安全性の根拠とした公開鍵暗号の一つである。 暗号 1 と デジタル署名 を実現できる方式として最初に公開された

この後も、ナップザック問題を利用した暗号は開発されていますが、優れたも のはできていません。 RSA暗号 RSA 暗号とは次のようなものです。 ふたつの大きな素数 p,q に対して、積を n とします。 また、φ(n)=(p1)(q1) とし、 φ(n) と互いに素な任意の数 e をはじめに 「暗号アルゴリズム10年問題」とは • 05年に米国立標準技術研究所(NIST)が当時主流だった 暗号アルゴリズム(Triple DES, 1024ビットRSA, SHA1)を "10年末を目途に"次世代のものに移行する計画を発表 「暗号世代交代」の本質は • "暗号システムのリスクマネジメント"として対応すRSA暗号の安全性 • 公開鍵nが素因数分解されるとp,qが求まる。 • 公開鍵eから、関係式 d =1/e mod (p1)(q1) により、秘密鍵dを求めることができる。 •RSA暗号の安全性は、素因数分解の困難性 に根拠を置いている。 15/28

例えば、rsa暗号は「素因数分解問題」が解けると秘密鍵が求まる Internet Week 08 資料 公開鍵暗号・デジタル署名の安全性Sep 30, 19 · rsa暗号とは、素因数分解の難しさを利用した暗号アルゴリズムのことです。セキュリティ対策を考える中で、暗号化の仕組みが気になっている人は多いでしょう。 この記事ではrsa暗号の概要から暗号化と復号の流れ、そして応用例まで解説します。暗号アルゴリズムの10年問題 • 暗号アルゴリズムの10年問題 – 現在主流となっている暗号アルゴリズム（トリプ ルdes，鍵長1,024ビットのrsa，sha1）をど のようにしてより安全なものに移行していくか． • 本問題の背景

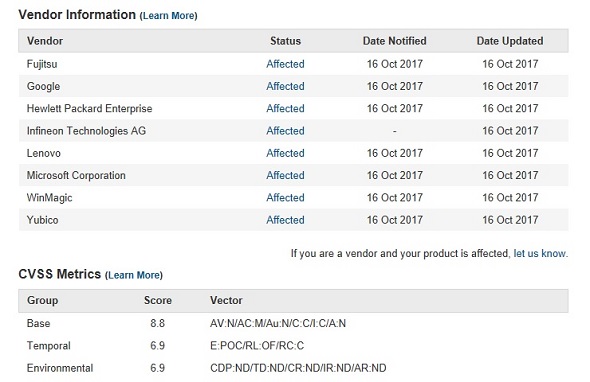
セキュリティチップにrsa暗号鍵の脆弱性 Googleやmicrosoftの製品にも影響 Itmedia エンタープライズ

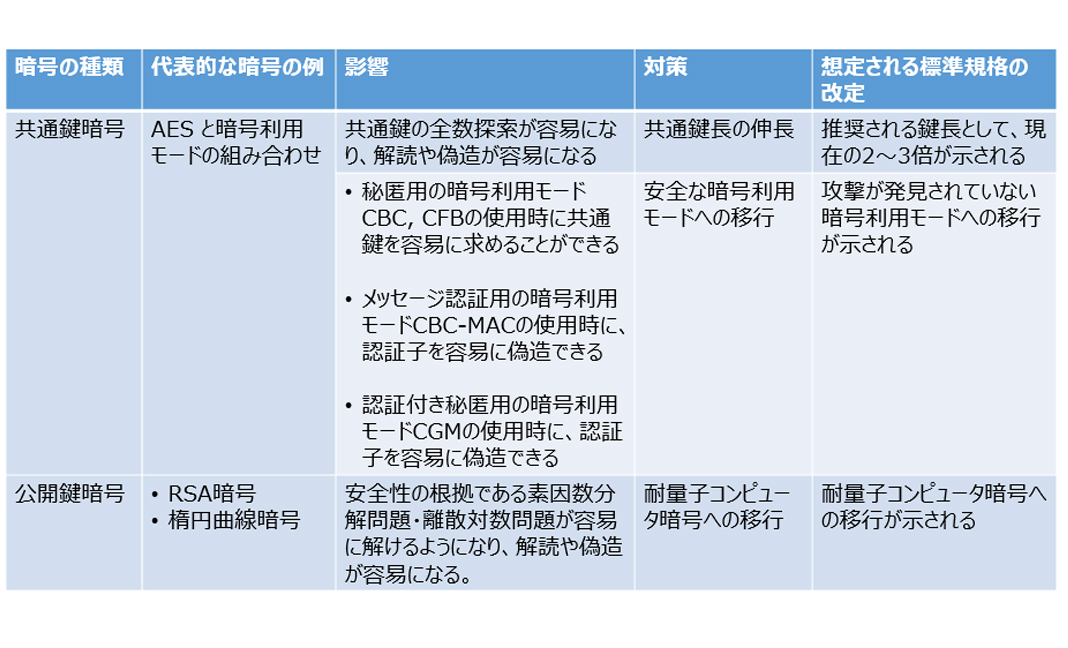
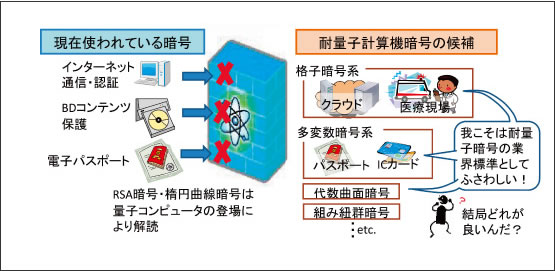
量子コンピュータによる暗号解読の可能性 Nttデータ

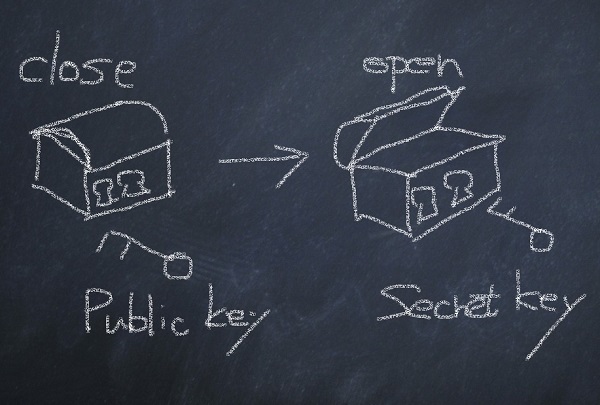
RSA暗号の 公開鍵の正体 は、2つの数字を掛け合わせて作られた 数字 です。 そして、公開鍵を2つの数字に分解し、それを ある公式 に入れれば、秘密鍵が求まってしまいます。 では、なぜ、公開鍵から秘密鍵がばれてしまうという、暗号としては致命的とも思われる欠点を持つ、RSA暗号が使われているかというと まず、現在では、暗号の研究と、「計算機」の高元々 rsa暗号とは､桁数が大きい合成数の素因数分解問題が困難である事を安全性の根拠とした公開鍵暗号の一つ です。 1977年に発明され､発明者であるR•L• R ivest､A• S hamir､L• A dlemanの頭文字を繋げ､名付けられた。公開鍵暗号の例 RSA暗号 Rivest, Shamir, Adleman (1977) † 大きな素数p;q を選び、積N = pq を作る † N を用いて、公開鍵e・秘密鍵d の対を作る † 暗号化の計算はN と公開鍵e とから可能 † 復号は秘密鍵d を用いる † N と公開鍵e とから秘密鍵d を求めるには、 N の素因子分解N = pq が必要

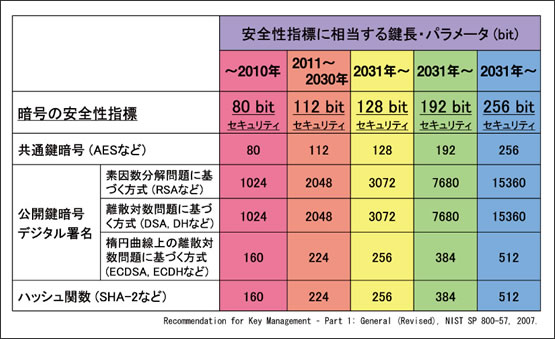
Nict News

Fpga で作る暗号は危険 5 Acri Blog

秘密鍵で暗号化された文章を復号 rsa_key = RSAconstruct((p*q, E, d)) #もちろんrsa_key = RSAconstruct((N, E, d))でもOK >>> rsa_key >>> rsa_keydecrypt(C) int = rsaそのコラム5には、rsa の公開鍵と暗号文が懸賞問題として載りました。 n が 10 進数 129 桁あることから、この問題は RSA129 という名で知られるようになりました。RSA暗号の仕組みとは？ 作り方や解き方・安全性までわかりやすく解説します 19 12/14 数学A こんにちは、ウチダショウマです。 「 RSA暗号 」とは、現代のネット社会を支えている最重要の暗号です。 例題 p = 3 p = 3 ， q = 11 q = 11 という 2 2 つの素数を使って、 X = 8 X = 8 という情報をRSA暗号化しなさい。 また、復号してしっかり 8 8 に戻るか

5 Rsa暗号 素因数分解の困難性を利用した暗号 Ppt Download

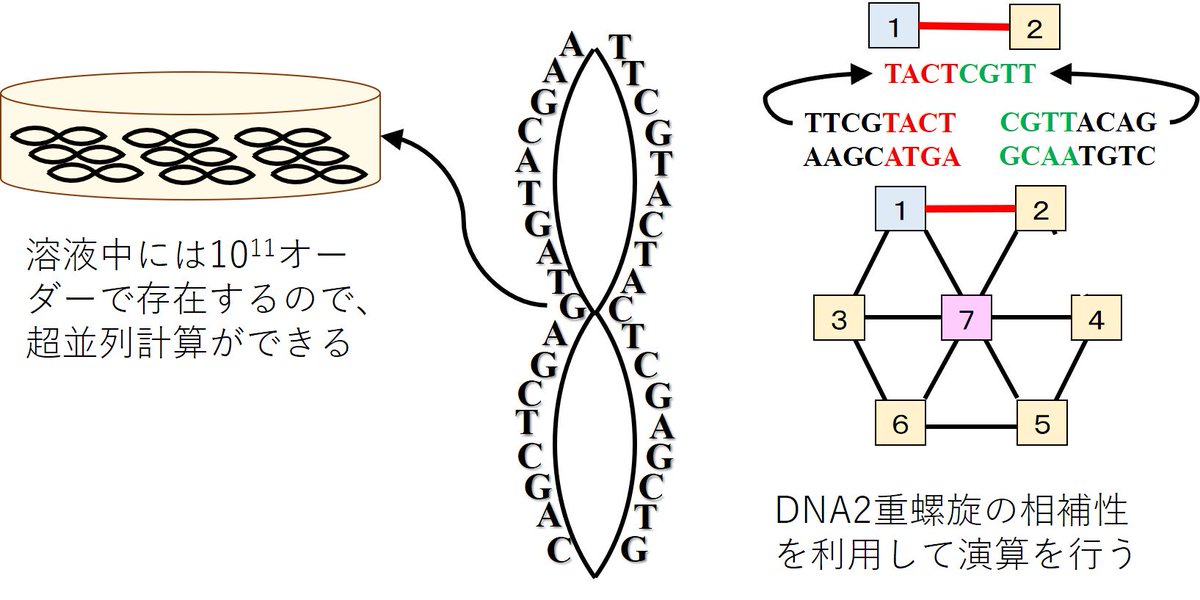
Cyclops Auf Twitter 今日は計算機科学者 レオナルド エイデルマン の誕生日 公開鍵型暗号の一つである Rsa暗号 の発案者として名高い Dnaコンピューティング の父とも言われるように Dna計算により Np完全問題 である ハミルトン閉路問題 を解いた

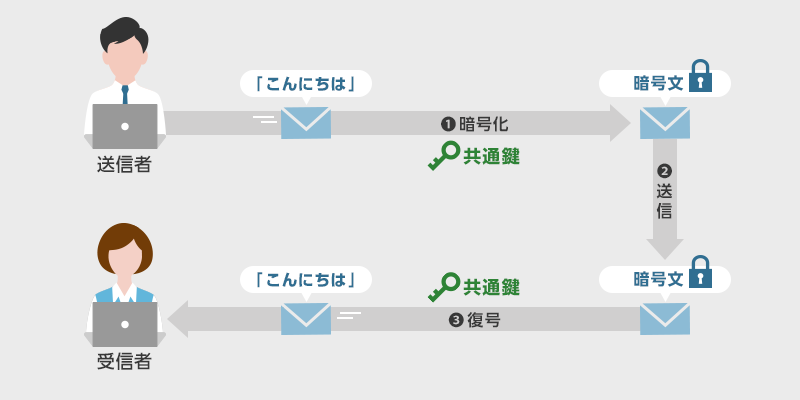
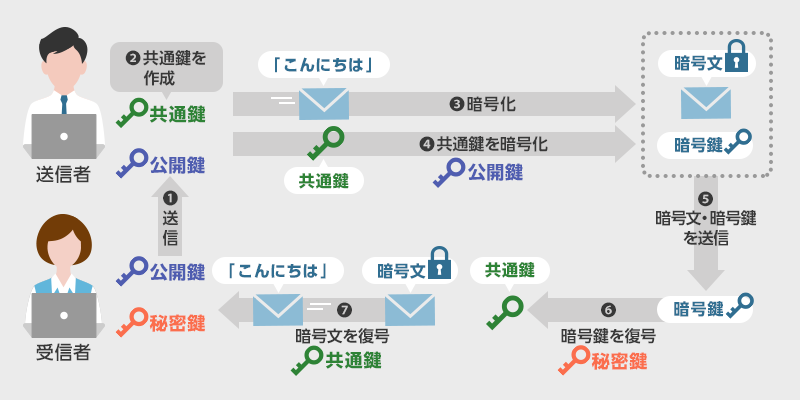
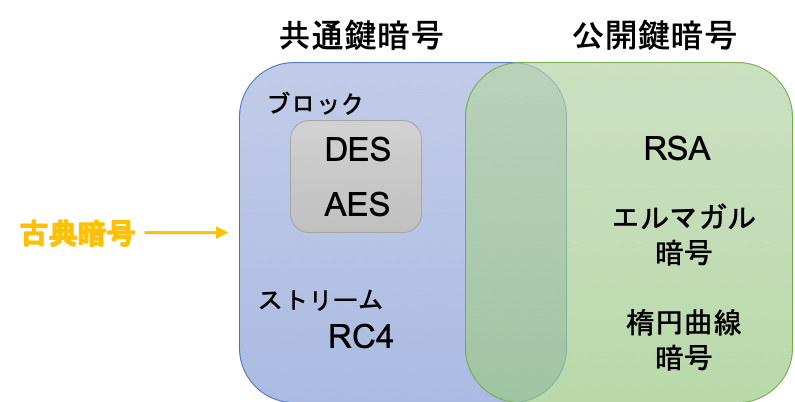
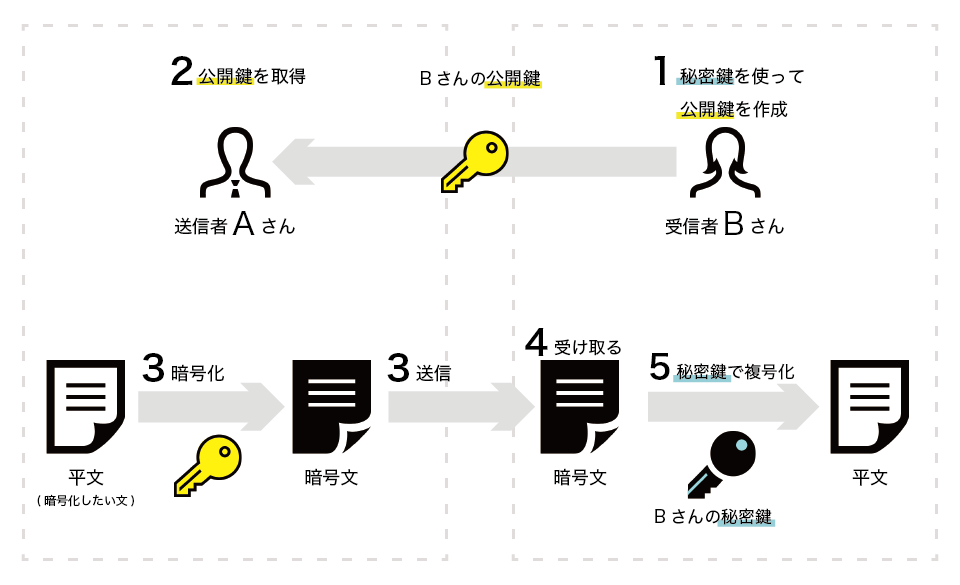
共通鍵暗号の問題点 共通鍵暗号の場合，あらかじめ送信者と受信者で共通鍵を共有しておく必要があります。 悪いやつに盗み見られても復号できないために暗号化を用いるのに， あらかじめ他人にバレないように共通鍵を共有する という行為が矛盾してRSA暗号とは、桁数が大きい合成数の素因数分解問題が困難であることを安全性の根拠とした公開鍵暗号の一つである。 RSA暗号 Wikipedia より RSAでは N には桁数が大きい素数 p 、 q の合成数を選RSA暗号の例 公開鍵・秘密鍵の生成 ①p = 5, q = 11 とするとn = pq = 55 となる。 ②k = LCM(p1,q1) = LCM(4,10) = となる。k と最大 公約数が1 となな数る正整数としてe = 3 を選を選 。 ぶ。 (e,n)=(3,55) を公開鍵とする。③③ed mod k = 3 d mod=1mod = 1 よりより d =7= 7 をを 秘密鍵秘密鍵 とするとする 。

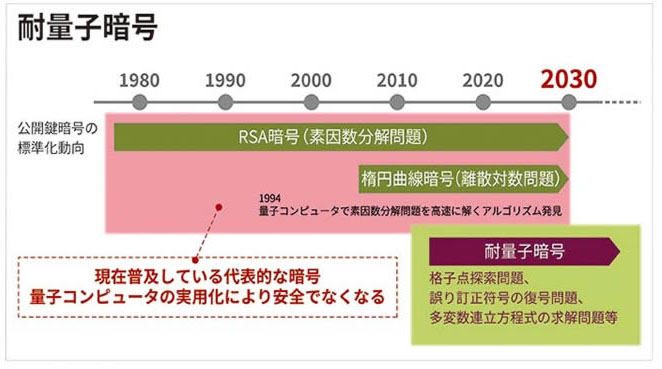
量子コンピュータの実用化と耐量子暗号の標準化動向 Sqat Jp

Ppt 暗号技術の国際動向について ー Aes 秘密鍵暗号 楕円公開鍵暗号 Powerpoint Presentation Id

RSA暗号の鍵生成手順 （1）相異なる素数pとqを選ぶ。 次のxに正整数を代入して計算すると、xより大きい素数のなかで最小のものを計算します。 同じ値の場合はx自身が素数です。選んだ素数を使う場合は下のp,qのボタンをクリックして下さい。May 12, 17 · 今日は有名なrsa暗号問題について見ていきたい。 まず、RSA暗号はいわゆる「公開鍵暗号」、すなわち暗号化に公開鍵を用いて、復号化には秘密鍵を用いることで、お互いに保持しなければならない秘密の鍵というものをなくすことができる。， rsa 暗号を解読する 方法は見つ かっ ていない ことから ， 素因数分解問 題は ， rsa 暗号の安全性の根拠であるとされて い る．ただし，rsa 暗号の安全性が真に素因数 分解問題と本当に等価であるかどうかにつ いては， 現時点でまだ示されてい ない． 3 数体篩法

Rsa暗号とは 仕組みをわかりやすく解説 プログラム付き じゃぱざむ

Rsa Dsa Ecdsa 電子署名

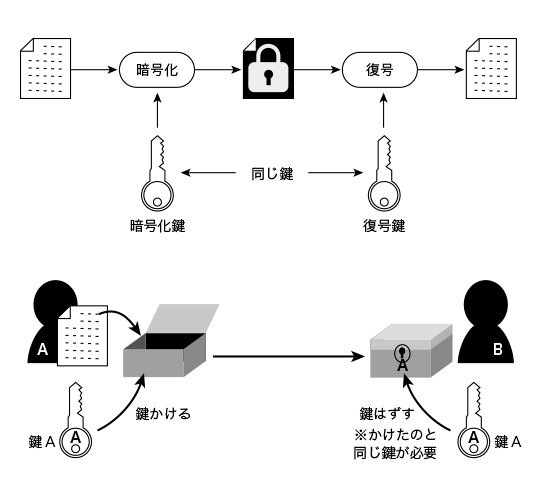
RubyでRSA暗号 ここからはコードを使って実際にRSA暗号をかけて、それを復号してみる。 文字は数字に変換 まず暗号では基本的に全ての文字が数字に置き換えられる。 "Jabba the Hutt"と書かれた文字列の数字変換はRubyであればeach_codepointを使えばできる。Oct 29,  · 楕円曲線を利用した暗号アルゴリズムでは、楕円曲線上の離散対数問題を暗号化の安全性の根拠としています。楕円曲線暗号は、rsa暗号に比べ、鍵長が短くても安全性を確保できるため、低いスペックのコンピューターでも使えるという利点があります。暗号とは ♦ 情報を送る際、送信者，受信者以外の 人物が、その情報の内容を理解することが 困難となるように構成されたもの （葉書の内容ならば、郵便局員にばれる） ♦ 重要な情報を送るためには、暗号の技術 が必要不可欠

サマーウォーズの２０５６桁の暗号 ｒの研究室

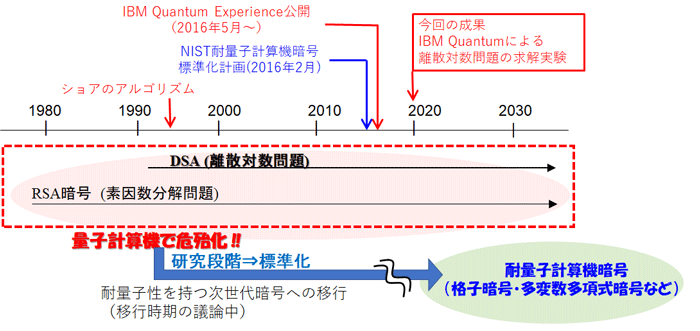
量子コンピュータ実機を用いた離散対数問題の求解実験に成功 Nict 情報通信研究機構

Oct 13, 11 · 「暗号と暗号史」8回目は、有史以来の課題だった「鍵」の配送を解決に導いたデフィー・ヘルマンの鍵配送とrsa暗号の誕生、これらを秘密裏に開発していた英国の動きを紹介する。Javaでrsa暗号を使う際にcryptrec暗号リストに足元をすくわれる可能性を回避する 投稿日：19年6月27日 更新日： 19年7月24日 標準的な暗号しか使わないケースでもJavaでRSAを使う時はBouncyCastleを入れておいた方が無難、という話です。

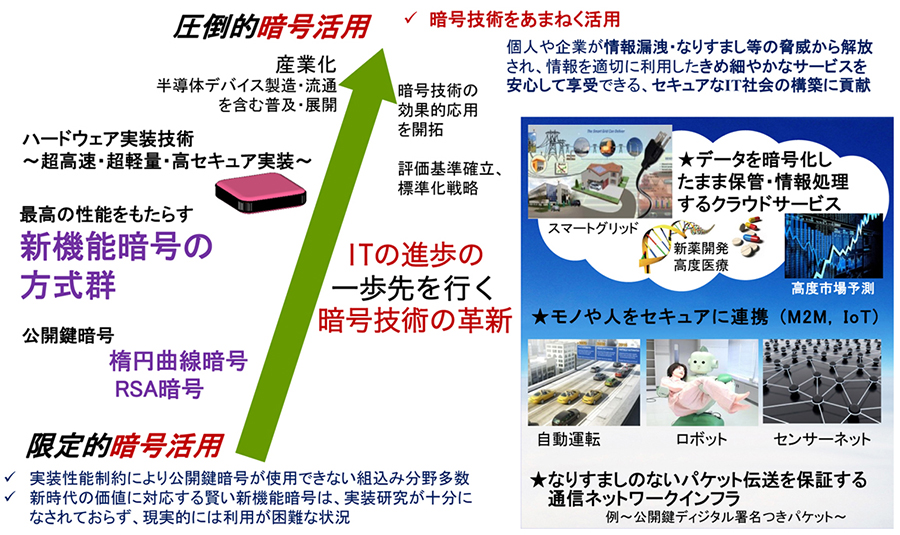
助成研究者情報 松本勉先生２ 安全安心な科学技術の振興 セコム科学技術振興財団

Rsa暗号の仕組みとは 作り方や解き方 安全性までわかりやすく解説します 遊ぶ数学塾

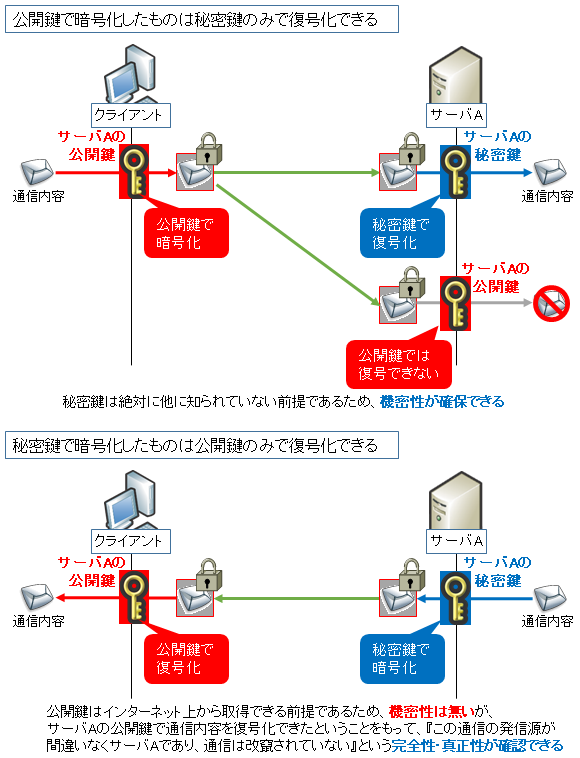
図解 初心者も分かる 公開鍵 秘密鍵 の仕組み 公開鍵暗号方式の身近で具体的な利用例やメリット Seの道標

公開鍵暗号アルゴリズム Moxbox

Ascii Jp Rsaから連なる暗号化技術の進化の歴史 秘密を守る人と暴く人の知恵比べ

Rsa の計算例

暗号のしくみと素因数分解 その２ 9 11更新 Rsa暗号のアルゴリズム 象が転んだ

総合ゼミナールｃ Rsa暗号

公開鍵暗号システム Rsa暗号 ８分 おまけ５分 Youtube

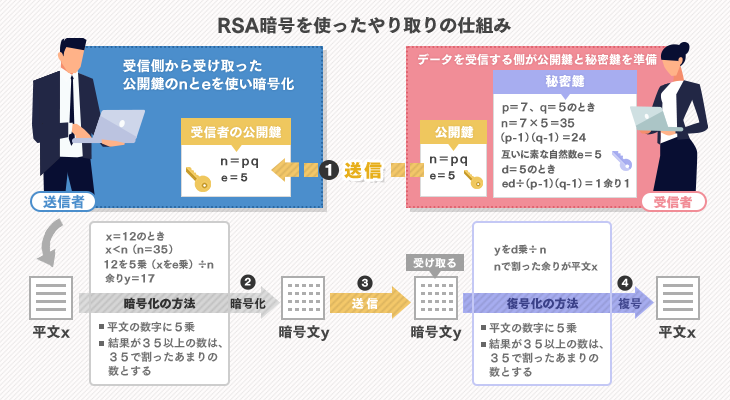
Rsa暗号とは 仕組みや応用事例を初心者にもわかりやすく解説 Itトレンド

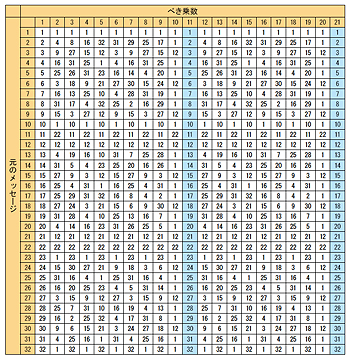
数学理論が情報社会を陰で支えるー暗号のしくみを考えてみようー サイエンス テクノロジー 研究 社会連携 京都産業大学

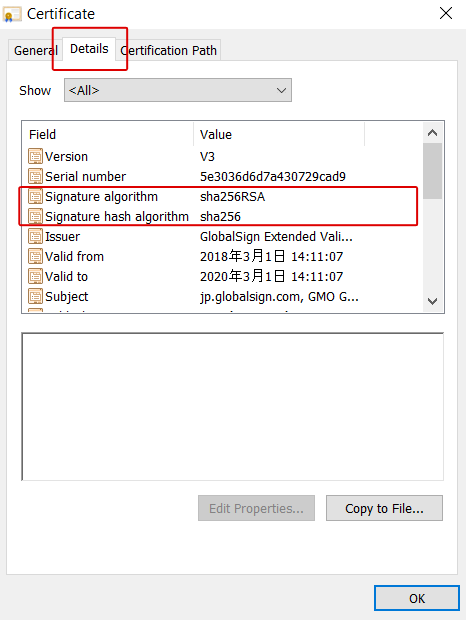
暗号化とは Gmoグローバルサイン 公式

基礎から学ぶ整数論 Rsa暗号入門 コロナ社

公開鍵暗号方式 Thoth Children

公開鍵暗号 D Space Atwiki アットウィキ

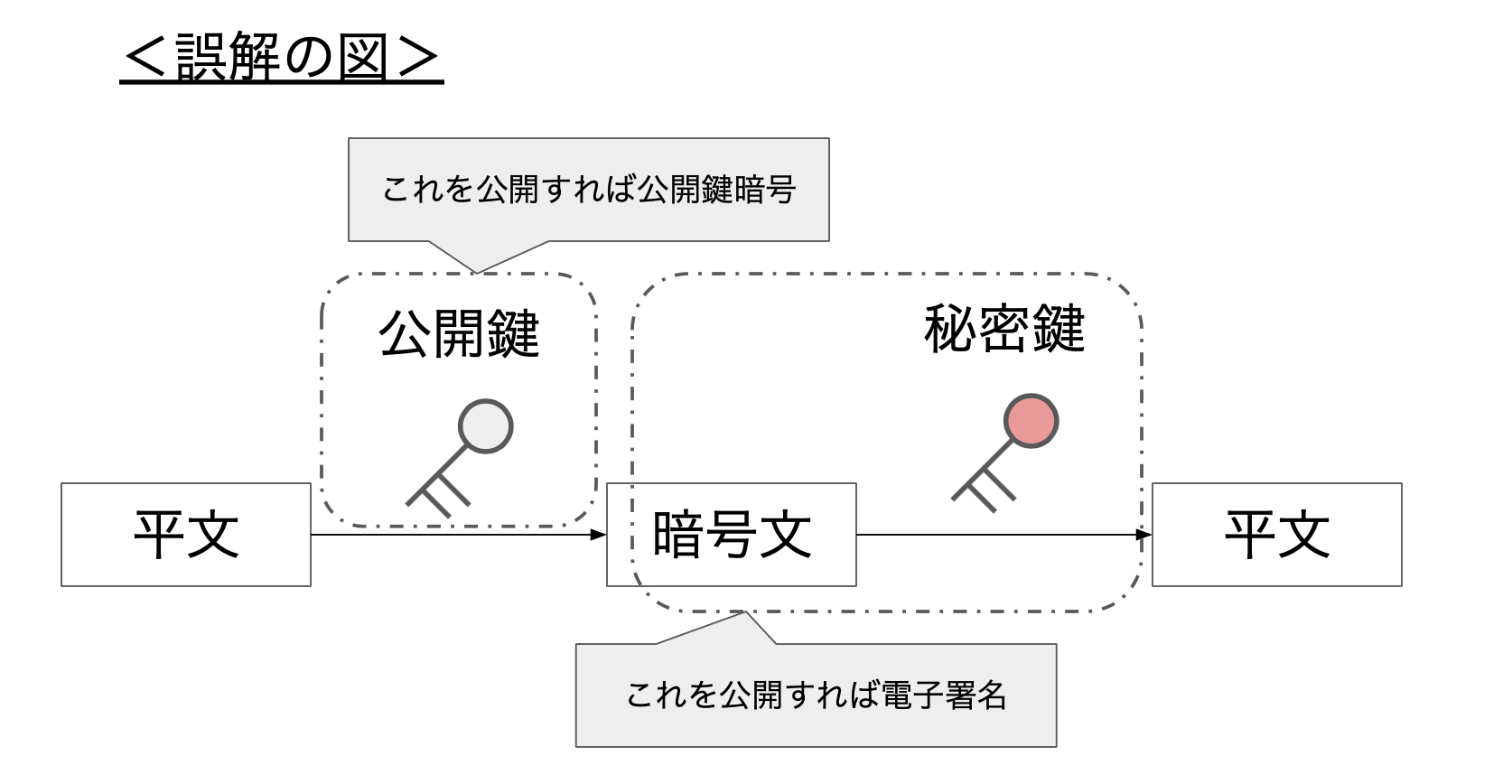
私は公開鍵暗号方式と電子署名を理解できていなかったようです まえおき By Hashhub Space Gbec Tech Blog Medium

Rsa暗号の原理

Rsa暗号解読問題を解く 後編 Ctf For Beginners 18 Rsa Is Power Mawalog

公開鍵暗号とrsa暗号の仕組み Qiita

Rsaをはじめとした暗号化の仕組みと方式の違いとは サイバーセキュリティ情報局

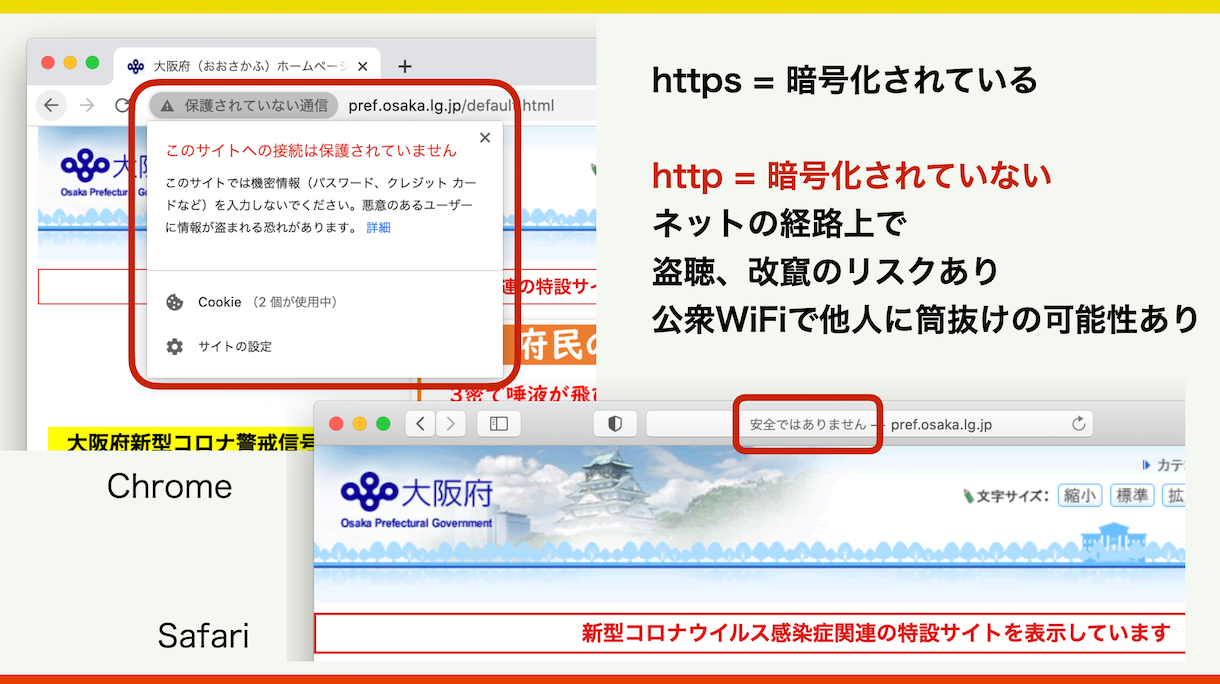
Webの信用と鍵の寿命 デジタル時代のhanko 公開鍵暗号の実装変更 Rsa Ed Dxgov Js Opendata 福野泰介の一日一創 Create Every Day By Taisuke Fukuno

公開鍵暗号 D Space Atwiki アットウィキ

Nict News

Ppt Rsa 暗号の多変数化と 連立代数方程式 Powerpoint Presentation Id

Rsa暗号運用でやってはいけない N のこと Ssmjp

Rsa 暗号がようやく分かった気がしたのでまとめてみる Tsujimotterのノートブック

量子コンピューターの登場によってもrsa暗号システムは破られないかもしれない Gigazine

Nttなど 公開鍵暗号の素因数分解問題で768ビット整数の分解に成功 日経クロステック Xtech

Rsa暗号の仕組みと安全性 高校数学の美しい物語

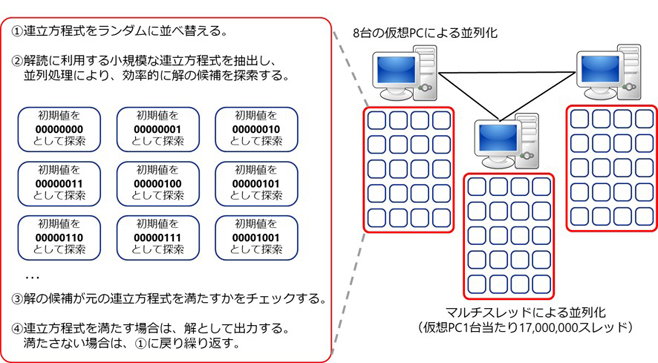
世界初 1161次元の符号暗号を解読 株式会社kddi総合研究所

賞金１億円のミレニアム懸賞問題とビットコイン Yybazaar

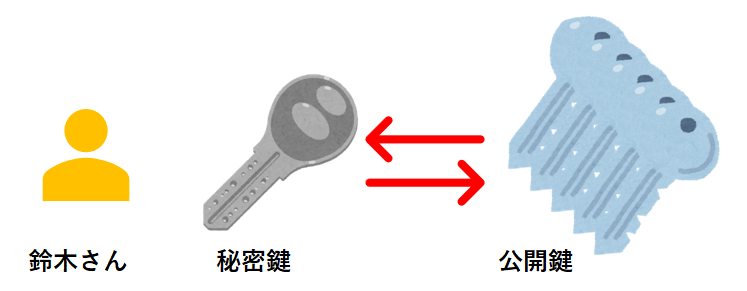
公開鍵暗号方式について解説します 情報処理試験で出された問題もまとめました たいらのエンジニアノート

量子コンピューターの登場によってもrsa暗号システムは破られないかもしれない Gigazine

電子署名と公開鍵暗号方式 電子署名 認証センター

グーグル 48ビットrsa暗号化キーへのアップグレードを完了 Cnet Japan

演習や小テスト Des Rsa暗号に関する計算問題 と似た問題は出題しません Ppt Download

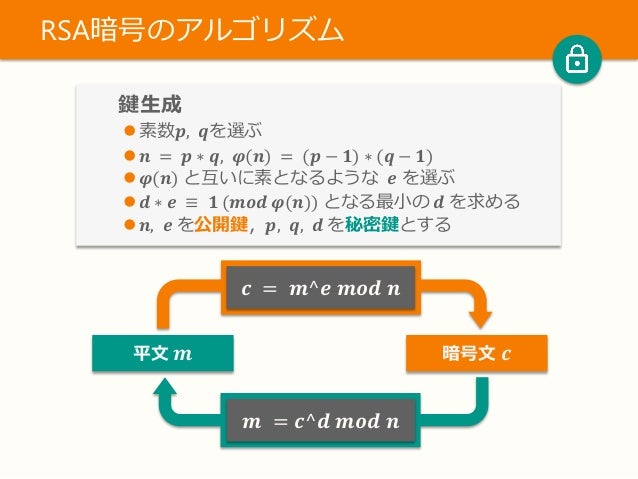
Rsa暗号運用でやってはいけない N のこと Ssmjp

Pki関連技術に関するコンテンツ

Rsaをはじめとした暗号化の仕組みと方式の違いとは サイバーセキュリティ情報局

連載 暗号と暗号史 第8回 有史以来の課題を解決 公開鍵暗号 Rsa暗号 Hh News Reports ハミングヘッズ

セキュリティチップにrsa暗号鍵の脆弱性 Googleやmicrosoftの製品にも影響 Itmedia エンタープライズ

暗号 インターネットを守る数学 Viviたる重み

暗号の数学的基礎 丸善出版 理工 医学 人文社会科学の専門書出版社

数学が役に立っている Rsa暗号の仕組みを解説 合同式とrsa暗号 第8回 Youtube

中学数学からはじめる暗号入門 現代の暗号はどのようにして作られたのか 書籍案内 技術評論社

Pentio Usb Token 3300tp Usbトークン ペンティオ 株

耐量子暗号を図解 量子コンピュータに解読されない 格子暗号 ってどんな仕組み 三津村直貴の 今さら聞けない テクノロジー講座 ビジネス It

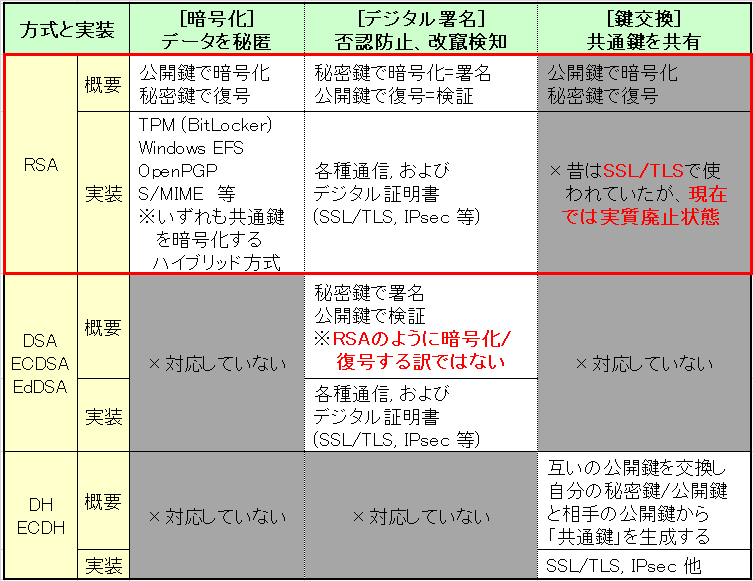
図解 初心者も分かる 公開鍵 秘密鍵 の仕組み 公開鍵暗号方式の身近で具体的な利用例やメリット Seの道標

Gnupg 0

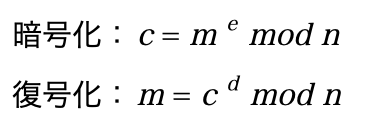
私は公開鍵暗号方式と電子署名を理解できていなかったようです まえおき By Hashhub Space Gbec Tech Blog Medium

公開鍵暗号について

Rsa暗号ってなに Runtime

1 前回の練習問題 F 29 1 2 28 において G 11 が生成元であることを確 かめ F 29 の元とその離散対数との関係を図示せよ X 1 28 に対し G X Mod 29 を計算すればよい Ppt Download

本気で考えてみた サマーウォーズのパスワードの暗号の解き方 56桁の暗号は解けるのか ぐだぐだプログラム日記

公開鍵暗号について

Pki関連技術に関するコンテンツ

サマーウォーズの暗号は京大生レベルの数学でも解けるのか

初学者向け 情報セキュリティ 暗号と認証その１ Beginaid

Rsa暗号とは 仕組みや応用事例を初心者にもわかりやすく解説 Itトレンド

量子コンピューターが暗号技術を 破壊 する その真偽を検証してみた 日経クロステック Xtech

公開鍵暗号方式とは 初心者でもわかる公開鍵暗号方式の基礎 Udemy メディア

数学が役に立っている Rsa暗号の仕組みを解説 合同式とrsa暗号 第8回 Youtube

4枚の図解でわかる公開鍵暗号 パーソルテクノロジースタッフ株式会社

量子コンピューター時代の暗号通信 24年にも民間企業で対策開始 ビジネスネットワーク Jp

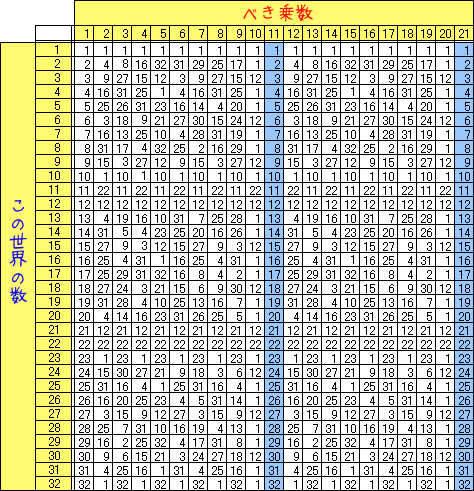
本気で考えてみた サマーウォーズのパスワードの暗号の解き方 56桁の暗号は解けるのか ぐだぐだプログラム日記

数学が守る私たちの秘密情報 中高生のための学会 サイエンスキャッスル By リバネス

暗号化とは Gmoグローバルサイン 公式

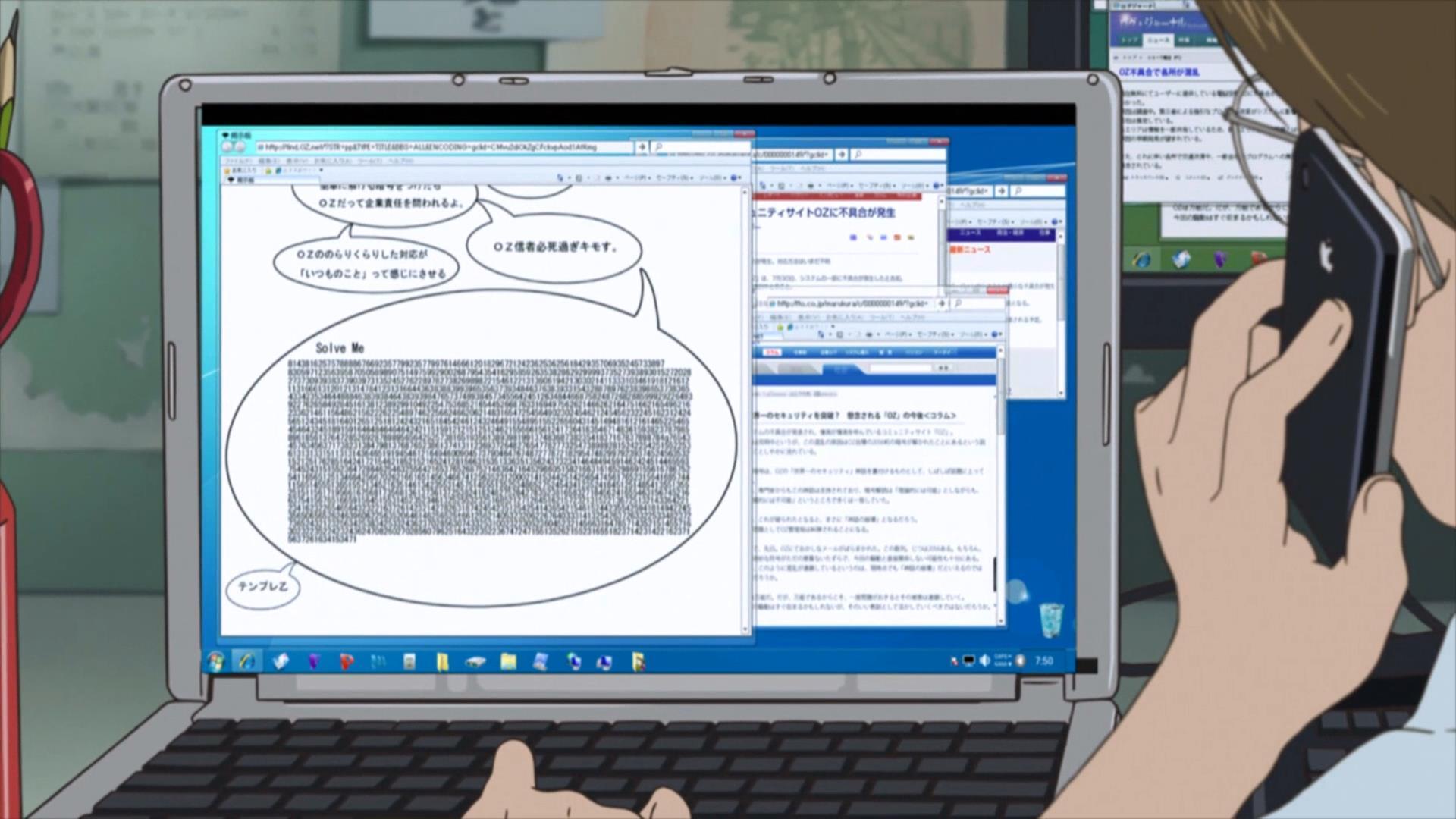
本気で考えてみた サマーウォーズのパスワードの暗号の解き方 56桁の暗号は解けるのか ぐだぐだプログラム日記

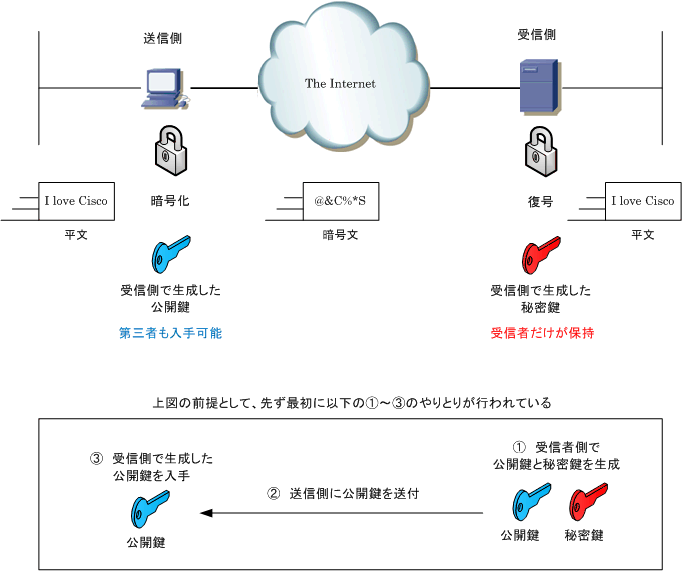
共通鍵暗号と公開鍵暗号とは

Bkpctfのrsa暗号問題を解く Sonickun Log

Rsaの公開鍵暗号のアルゴリズム4つ Rsa暗号の安全性について2つ テックマガジン From Fenetインフラ

Arigirisu14 Rsa

Rsa暗号の仕組みと安全性 高校数学の美しい物語

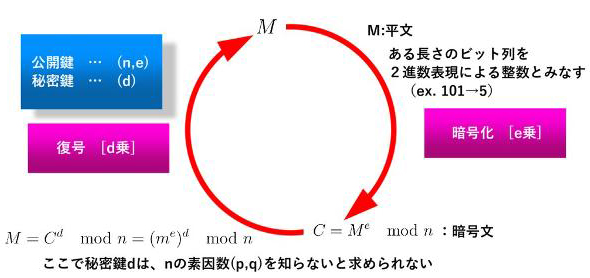
Rsaとは Rsa暗号とは It

サマーウォーズの暗号は京大生レベルの数学でも解けるのか

公開鍵暗号 D Space Atwiki アットウィキ

Rsa暗号運用でやってはいけない N のこと Ssmjp

Rsa暗号の仕組みとは 作り方や解き方 安全性までわかりやすく解説します 遊ぶ数学塾

Rsa暗号からの脱出 Tsujimotterのノートブック

2つの公開鍵暗号 公開鍵暗号の基礎知識 Qiita

公開鍵暗号について

ちょっと得する知識シリーズ 1 素因数分解を知れば暗号が分かる 1 Tech

Incoming Term: rsa暗号 問題,